Label guide#
Basic labelling#
All ArviZ plotting functions and some stats functions can take an optional labeller argument.
By default, labels show the variable name.
Multidimensional variables also show the coordinate value.
Example: Default labelling#
In [1]: import arviz as az
...: schools = az.load_arviz_data("centered_eight")
...: az.summary(schools)
...:
Out[1]:
mean sd hdi_3% ... ess_bulk ess_tail r_hat
mu 4.486 3.487 -1.623 ... 241.0 659.0 1.02
theta[Choate] 6.460 5.868 -4.564 ... 365.0 710.0 1.01
theta[Deerfield] 5.028 4.883 -4.311 ... 427.0 851.0 1.01
theta[Phillips Andover] 3.938 5.688 -7.769 ... 515.0 730.0 1.01
theta[Phillips Exeter] 4.872 5.012 -4.490 ... 337.0 869.0 1.01
theta[Hotchkiss] 3.667 4.956 -6.470 ... 365.0 1034.0 1.01
theta[Lawrenceville] 3.975 5.187 -7.041 ... 521.0 1031.0 1.01
theta[St. Paul's] 6.581 5.105 -3.093 ... 276.0 586.0 1.01
theta[Mt. Hermon] 4.772 5.737 -5.858 ... 452.0 754.0 1.01
tau 4.124 3.102 0.896 ... 67.0 38.0 1.06
[10 rows x 9 columns]
ArviZ supports label based indexing powered by xarray. Through label based indexing, you can use labels to plot a subset of selected variables.
Example: Label based indexing#
For a case where the coordinate values shown for the theta variable coordinate to the school dimension,
you can indicate ArviZ to plot tau by including it in the var_names argument to inspect its 1.03 rhat() value.
To inspect the theta values for the Choate and St. Paul's coordinates, you can include theta in var_names and use the coords argument to select only these two coordinate values.
You can generate this plot with the following command:
In [2]: az.plot_trace(schools, var_names=["tau", "theta"], coords={"school": ["Choate", "St. Paul's"]}, compact=False);
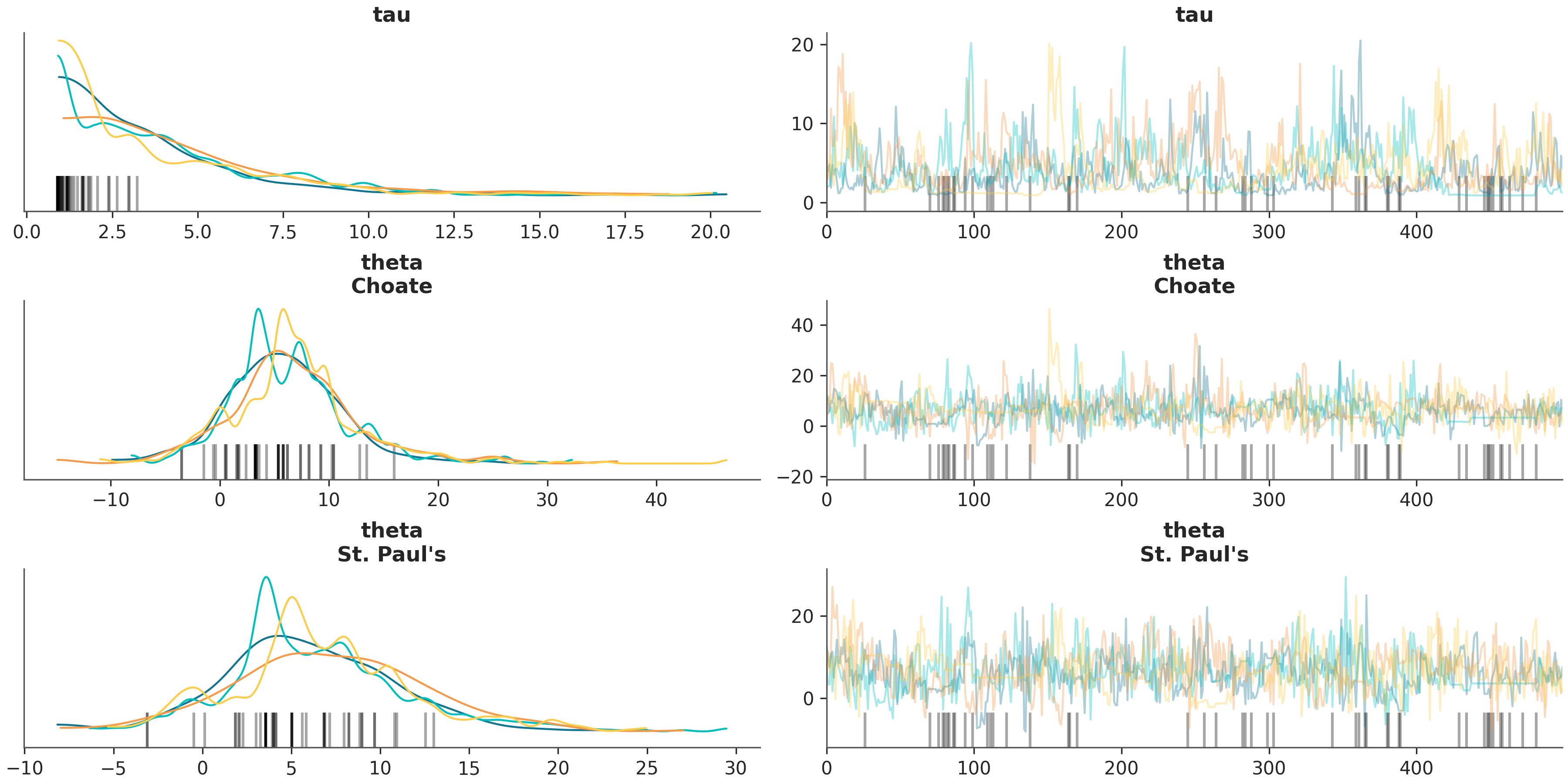
Using the above command, you can now identify issues for low tau values.
Example: Using the labeller argument#
You can use the labeller argument to customize labels.
Unlike the default labels that show theta, not \(\theta\) (generated from $\theta$ using \(\LaTeX\)), the labeller argument presents the labels with proper math notation.
You can use MapLabeller to rename the variable theta to $\theta$, as shown in the following example:
In [3]: import arviz.labels as azl
...: labeller = azl.MapLabeller(var_name_map={"theta": r"$\theta$"})
...: coords = {"school": ["Deerfield", "Hotchkiss", "Lawrenceville"]}
...:
In [4]: az.plot_posterior(schools, var_names="theta", coords=coords, labeller=labeller, ref_val=5);
See also
For a list of labellers available in ArviZ, see the the API reference page.
Sorting labels#
ArviZ allows labels to be sorted in two ways:
Using the arguments passed to ArviZ plotting functions
Sorting the underlying
xarray.Dataset
The first option is more suitable for single time ordering whereas the second option is more suitable for sorting plots consistently.
Note
Both ways are limited.
Multidimensional variables can not be separated.
For example, it is possible to sort theta, mu, or tau in any order, and within theta to sort the schools in any order, but it is not possible to sort half of the schools, then mu and tau and then the rest of the schools.
Sorting variable names#
In [5]: var_order = ["theta", "mu", "tau"]
For variable names to appear sorted when calling ArviZ functions, pass a sorted list of the variable names.
In [6]: az.summary(schools, var_names=var_order)
Out[6]:
mean sd hdi_3% ... ess_bulk ess_tail r_hat
theta[Choate] 6.460 5.868 -4.564 ... 365.0 710.0 1.01
theta[Deerfield] 5.028 4.883 -4.311 ... 427.0 851.0 1.01
theta[Phillips Andover] 3.938 5.688 -7.769 ... 515.0 730.0 1.01
theta[Phillips Exeter] 4.872 5.012 -4.490 ... 337.0 869.0 1.01
theta[Hotchkiss] 3.667 4.956 -6.470 ... 365.0 1034.0 1.01
theta[Lawrenceville] 3.975 5.187 -7.041 ... 521.0 1031.0 1.01
theta[St. Paul's] 6.581 5.105 -3.093 ... 276.0 586.0 1.01
theta[Mt. Hermon] 4.772 5.737 -5.858 ... 452.0 754.0 1.01
mu 4.486 3.487 -1.623 ... 241.0 659.0 1.02
tau 4.124 3.102 0.896 ... 67.0 38.0 1.06
[10 rows x 9 columns]
In xarray, subsetting the Dataset with a sorted list of variable names will order the Dataset.
In [7]: schools.posterior = schools.posterior[var_order]
...: az.summary(schools)
...:
Out[7]:
mean sd hdi_3% ... ess_bulk ess_tail r_hat
theta[Choate] 6.460 5.868 -4.564 ... 365.0 710.0 1.01
theta[Deerfield] 5.028 4.883 -4.311 ... 427.0 851.0 1.01
theta[Phillips Andover] 3.938 5.688 -7.769 ... 515.0 730.0 1.01
theta[Phillips Exeter] 4.872 5.012 -4.490 ... 337.0 869.0 1.01
theta[Hotchkiss] 3.667 4.956 -6.470 ... 365.0 1034.0 1.01
theta[Lawrenceville] 3.975 5.187 -7.041 ... 521.0 1031.0 1.01
theta[St. Paul's] 6.581 5.105 -3.093 ... 276.0 586.0 1.01
theta[Mt. Hermon] 4.772 5.737 -5.858 ... 452.0 754.0 1.01
mu 4.486 3.487 -1.623 ... 241.0 659.0 1.02
tau 4.124 3.102 0.896 ... 67.0 38.0 1.06
[10 rows x 9 columns]
Sorting coordinate values#
For sorting coordinate values, first, define the order, then store it, and use the result to sort the coordinate values. You can define the order by creating a list manually or by using xarray objects as illustrated in the below example “Sorting out the schools by mean”.
Example: Sorting the schools by mean#
Locate the means of each school by using the following command:
In [8]: school_means = schools.posterior["theta"].mean(("chain", "draw"))
...: school_means
...:
Out[8]:
<xarray.DataArray 'theta' (school: 8)>
array([6.46006423, 5.02755458, 3.93803067, 4.87161236, 3.66684116,
3.97468712, 6.58092358, 4.77241104])
Coordinates:
* school (school) object 'Choate' 'Deerfield' ... "St. Paul's" 'Mt. Hermon'
You can use the
DataArrayresult to sort the coordinate values fortheta.
There are two ways of sorting:
Arviz args
xarray
Sort the coordinate values to pass them as a coords argument and choose the order of the rows.
In [9]: sorted_schools = schools.posterior["school"].sortby(school_means)
...: az.summary(schools, var_names="theta", coords={"school": sorted_schools})
...:
Out[9]:
mean sd hdi_3% ... ess_bulk ess_tail r_hat
theta[Hotchkiss] 3.667 4.956 -6.470 ... 365.0 1034.0 1.01
theta[Phillips Andover] 3.938 5.688 -7.769 ... 515.0 730.0 1.01
theta[Lawrenceville] 3.975 5.187 -7.041 ... 521.0 1031.0 1.01
theta[Mt. Hermon] 4.772 5.737 -5.858 ... 452.0 754.0 1.01
theta[Phillips Exeter] 4.872 5.012 -4.490 ... 337.0 869.0 1.01
theta[Deerfield] 5.028 4.883 -4.311 ... 427.0 851.0 1.01
theta[Choate] 6.460 5.868 -4.564 ... 365.0 710.0 1.01
theta[St. Paul's] 6.581 5.105 -3.093 ... 276.0 586.0 1.01
[8 rows x 9 columns]
You can use the sortby() method to order our coordinate values directly at the source.
In [10]: schools.posterior = schools.posterior.sortby(school_means)
....: az.summary(schools, var_names="theta")
....:
Out[10]:
mean sd hdi_3% ... ess_bulk ess_tail r_hat
theta[Hotchkiss] 3.667 4.956 -6.470 ... 365.0 1034.0 1.01
theta[Phillips Andover] 3.938 5.688 -7.769 ... 515.0 730.0 1.01
theta[Lawrenceville] 3.975 5.187 -7.041 ... 521.0 1031.0 1.01
theta[Mt. Hermon] 4.772 5.737 -5.858 ... 452.0 754.0 1.01
theta[Phillips Exeter] 4.872 5.012 -4.490 ... 337.0 869.0 1.01
theta[Deerfield] 5.028 4.883 -4.311 ... 427.0 851.0 1.01
theta[Choate] 6.460 5.868 -4.564 ... 365.0 710.0 1.01
theta[St. Paul's] 6.581 5.105 -3.093 ... 276.0 586.0 1.01
[8 rows x 9 columns]
Sorting dimensions#
In some cases, our multidimensional variables may not have only one more dimension (a length n dimension
in addition to the chain and draw ones)
but could have multiple more dimensions.
Let’s imagine we have performed a set of fixed experiments on several days to multiple subjects,
three data dimensions overall.
We will create fake inference data with data mimicking this situation to show how to sort dimensions.
To keep things short and not clutter the guide too much with unnecessary output lines,
we will stick to a posterior of a single variable and the dimension sizes will be 2, 3, 4.
In [11]: from numpy.random import default_rng
....: import pandas as pd
....: rng = default_rng()
....: samples = rng.normal(size=(4, 500, 2, 3, 4))
....: coords = {
....: "subject": ["ecoli", "pseudomonas", "clostridium"],
....: "date": ["1-3-2020", "2-4-2020", "1-5-2020", "1-6-2020"],
....: "experiment": [1, 2]
....: }
....: experiments = az.from_dict(
....: posterior={"b": samples}, dims={"b": ["experiment", "subject", "date"]}, coords=coords
....: )
....: experiments.posterior
....:
Out[11]:
<xarray.Dataset>
Dimensions: (chain: 4, draw: 500, experiment: 2, subject: 3, date: 4)
Coordinates:
* chain (chain) int64 0 1 2 3
* draw (draw) int64 0 1 2 3 4 5 6 7 ... 492 493 494 495 496 497 498 499
* experiment (experiment) int64 1 2
* subject (subject) <U11 'ecoli' 'pseudomonas' 'clostridium'
* date (date) <U8 '1-3-2020' '2-4-2020' '1-5-2020' '1-6-2020'
Data variables:
b (chain, draw, experiment, subject, date) float64 1.632 ... -0...
Attributes:
created_at: 2023-07-18T19:57:15.900247
arviz_version: 0.16.1
Given how we have constructed our dataset, the default order is experiment, subject, date.
Click to see the default summary
In [12]: az.summary(experiments)
Out[12]:
mean sd hdi_3% ... ess_bulk ess_tail r_hat
b[1, ecoli, 1-3-2020] -0.027 1.019 -1.771 ... 1931.0 2008.0 1.0
b[1, ecoli, 2-4-2020] 0.024 0.999 -1.816 ... 2032.0 1775.0 1.0
b[1, ecoli, 1-5-2020] 0.030 1.005 -1.665 ... 2002.0 1666.0 1.0
b[1, ecoli, 1-6-2020] -0.013 0.986 -1.915 ... 2010.0 1932.0 1.0
b[1, pseudomonas, 1-3-2020] 0.001 1.001 -2.024 ... 2050.0 1737.0 1.0
b[1, pseudomonas, 2-4-2020] 0.009 0.998 -1.871 ... 1899.0 1698.0 1.0
b[1, pseudomonas, 1-5-2020] 0.016 1.000 -1.933 ... 2118.0 2013.0 1.0
b[1, pseudomonas, 1-6-2020] 0.034 0.985 -1.901 ... 1902.0 1846.0 1.0
b[1, clostridium, 1-3-2020] 0.020 0.979 -1.765 ... 1991.0 2016.0 1.0
b[1, clostridium, 2-4-2020] -0.021 0.993 -1.965 ... 1965.0 1893.0 1.0
b[1, clostridium, 1-5-2020] -0.052 0.985 -1.981 ... 1872.0 1713.0 1.0
b[1, clostridium, 1-6-2020] -0.016 0.993 -1.892 ... 1926.0 1891.0 1.0
b[2, ecoli, 1-3-2020] 0.029 1.003 -2.062 ... 1966.0 1973.0 1.0
b[2, ecoli, 2-4-2020] -0.010 1.003 -1.944 ... 1737.0 1820.0 1.0
b[2, ecoli, 1-5-2020] 0.017 1.002 -1.759 ... 1869.0 1934.0 1.0
b[2, ecoli, 1-6-2020] -0.017 1.014 -1.984 ... 2008.0 2016.0 1.0
b[2, pseudomonas, 1-3-2020] -0.046 1.001 -1.926 ... 1807.0 1868.0 1.0
b[2, pseudomonas, 2-4-2020] 0.043 0.997 -1.768 ... 1700.0 1706.0 1.0
b[2, pseudomonas, 1-5-2020] 0.017 1.006 -1.814 ... 2024.0 1913.0 1.0
b[2, pseudomonas, 1-6-2020] -0.024 0.998 -1.967 ... 1856.0 1972.0 1.0
b[2, clostridium, 1-3-2020] -0.001 1.000 -1.868 ... 1680.0 1928.0 1.0
b[2, clostridium, 2-4-2020] -0.019 1.036 -2.220 ... 1929.0 1822.0 1.0
b[2, clostridium, 1-5-2020] -0.017 0.987 -1.847 ... 2063.0 1974.0 1.0
b[2, clostridium, 1-6-2020] -0.033 1.021 -1.904 ... 2062.0 1960.0 1.0
[24 rows x 9 columns]
However, the order we want is: subject, date, experiment.
Now, to get the desired result, we need to modify the underlying xarray object.
In [13]: dim_order = ("chain", "draw", "subject", "date", "experiment")
In [14]: experiments = experiments.posterior.transpose(*dim_order)
In [15]: az.summary(experiments)
Out[15]:
mean sd hdi_3% ... ess_bulk ess_tail r_hat
b[ecoli, 1-3-2020, 1] -0.027 1.019 -1.771 ... 1931.0 2008.0 1.0
b[ecoli, 1-3-2020, 2] 0.029 1.003 -2.062 ... 1966.0 1973.0 1.0
b[ecoli, 2-4-2020, 1] 0.024 0.999 -1.816 ... 2032.0 1775.0 1.0
b[ecoli, 2-4-2020, 2] -0.010 1.003 -1.944 ... 1737.0 1820.0 1.0
b[ecoli, 1-5-2020, 1] 0.030 1.005 -1.665 ... 2002.0 1666.0 1.0
b[ecoli, 1-5-2020, 2] 0.017 1.002 -1.759 ... 1869.0 1934.0 1.0
b[ecoli, 1-6-2020, 1] -0.013 0.986 -1.915 ... 2010.0 1932.0 1.0
b[ecoli, 1-6-2020, 2] -0.017 1.014 -1.984 ... 2008.0 2016.0 1.0
b[pseudomonas, 1-3-2020, 1] 0.001 1.001 -2.024 ... 2050.0 1737.0 1.0
b[pseudomonas, 1-3-2020, 2] -0.046 1.001 -1.926 ... 1807.0 1868.0 1.0
b[pseudomonas, 2-4-2020, 1] 0.009 0.998 -1.871 ... 1899.0 1698.0 1.0
b[pseudomonas, 2-4-2020, 2] 0.043 0.997 -1.768 ... 1700.0 1706.0 1.0
b[pseudomonas, 1-5-2020, 1] 0.016 1.000 -1.933 ... 2118.0 2013.0 1.0
b[pseudomonas, 1-5-2020, 2] 0.017 1.006 -1.814 ... 2024.0 1913.0 1.0
b[pseudomonas, 1-6-2020, 1] 0.034 0.985 -1.901 ... 1902.0 1846.0 1.0
b[pseudomonas, 1-6-2020, 2] -0.024 0.998 -1.967 ... 1856.0 1972.0 1.0
b[clostridium, 1-3-2020, 1] 0.020 0.979 -1.765 ... 1991.0 2016.0 1.0
b[clostridium, 1-3-2020, 2] -0.001 1.000 -1.868 ... 1680.0 1928.0 1.0
b[clostridium, 2-4-2020, 1] -0.021 0.993 -1.965 ... 1965.0 1893.0 1.0
b[clostridium, 2-4-2020, 2] -0.019 1.036 -2.220 ... 1929.0 1822.0 1.0
b[clostridium, 1-5-2020, 1] -0.052 0.985 -1.981 ... 1872.0 1713.0 1.0
b[clostridium, 1-5-2020, 2] -0.017 0.987 -1.847 ... 2063.0 1974.0 1.0
b[clostridium, 1-6-2020, 1] -0.016 0.993 -1.892 ... 1926.0 1891.0 1.0
b[clostridium, 1-6-2020, 2] -0.033 1.021 -1.904 ... 2062.0 1960.0 1.0
[24 rows x 9 columns]
Note
However, we don’t need to overwrite or store the modified xarray object.
Doing az.summary(experiments.posterior.transpose(*dim_order)) would work just the same
if we only want to use this order once.
Labeling with indexes#
As you may have seen, there are some labellers with Idx in their name:
IdxLabeller and DimIdxLabeller.
They show the positional index of the values instead of their corresponding coordinate value.
We have seen before that we can use the coords argument or
the sel() method to select data based on the coordinate values.
Similarly, we can use the isel() method to select data based on positional indexes.
In [16]: az.summary(schools, labeller=azl.IdxLabeller())
Out[16]:
mean sd hdi_3% hdi_97% ... mcse_sd ess_bulk ess_tail r_hat
theta[0] 3.667 4.956 -6.470 11.719 ... 0.185 365.0 1034.0 1.01
theta[1] 3.938 5.688 -7.769 13.676 ... 0.188 515.0 730.0 1.01
theta[2] 3.975 5.187 -7.041 12.209 ... 0.154 521.0 1031.0 1.01
theta[3] 4.772 5.737 -5.858 16.014 ... 0.182 452.0 754.0 1.01
theta[4] 4.872 5.012 -4.490 14.663 ... 0.187 337.0 869.0 1.01
theta[5] 5.028 4.883 -4.311 14.254 ... 0.164 427.0 851.0 1.01
theta[6] 6.460 5.868 -4.564 17.132 ... 0.213 365.0 710.0 1.01
theta[7] 6.581 5.105 -3.093 16.268 ... 0.210 276.0 586.0 1.01
mu 4.486 3.487 -1.623 10.693 ... 0.160 241.0 659.0 1.02
tau 4.124 3.102 0.896 9.668 ... 0.186 67.0 38.0 1.06
[10 rows x 9 columns]
After seeing the above summary, let’s use isel method to generate the summary of a subset only.
In [17]: az.summary(schools.isel(school=[2, 5, 7]), labeller=azl.IdxLabeller())
Out[17]:
mean sd hdi_3% hdi_97% ... mcse_sd ess_bulk ess_tail r_hat
theta[0] 3.975 5.187 -7.041 12.209 ... 0.154 521.0 1031.0 1.01
theta[1] 5.028 4.883 -4.311 14.254 ... 0.164 427.0 851.0 1.01
theta[2] 6.581 5.105 -3.093 16.268 ... 0.210 276.0 586.0 1.01
mu 4.486 3.487 -1.623 10.693 ... 0.160 241.0 659.0 1.02
tau 4.124 3.102 0.896 9.668 ... 0.186 67.0 38.0 1.06
[5 rows x 9 columns]
Warning
Positional indexing is NOT label based indexing with numbers!
The positional indexes shown will correspond to the ordinal position in the subsetted object.
If you are not subsetting the object, you can use these indexes with isel without problem.
However, if you are subsetting the data (either directly or with the coords argument)
and want to use the positional indexes shown, you need to use them on the corresponding subset.
Example: If you use a dict named coords when calling a plotting function,
for isel to work it has to be called on
original_idata.sel(**coords).isel(<desired positional idxs>) and
not on original_idata.isel(<desired positional idxs>).
Labeller mixtures#
In some cases, none of the available labellers do the right job.
For example, one case where this is bound to happen is with plot_forest().
When setting legend=True it does not really make sense to add the model name to the tick labels.
plot_forest knows that, and if no labeller is passed, it uses either
BaseLabeller or NoModelLabeller depending on the value of legend.
However, if we do want to use the labeller argument, we have to enforce this default ourselves:
In [18]: schools2 = az.load_arviz_data("non_centered_eight")
In [19]: az.plot_forest(
....: (schools, schools2),
....: model_names=("centered", "non_centered"),
....: coords={"school": ["Deerfield", "Lawrenceville", "Mt. Hermon"]},
....: figsize=(10,7),
....: labeller=azl.DimCoordLabeller(),
....: legend=True
....: );
....:
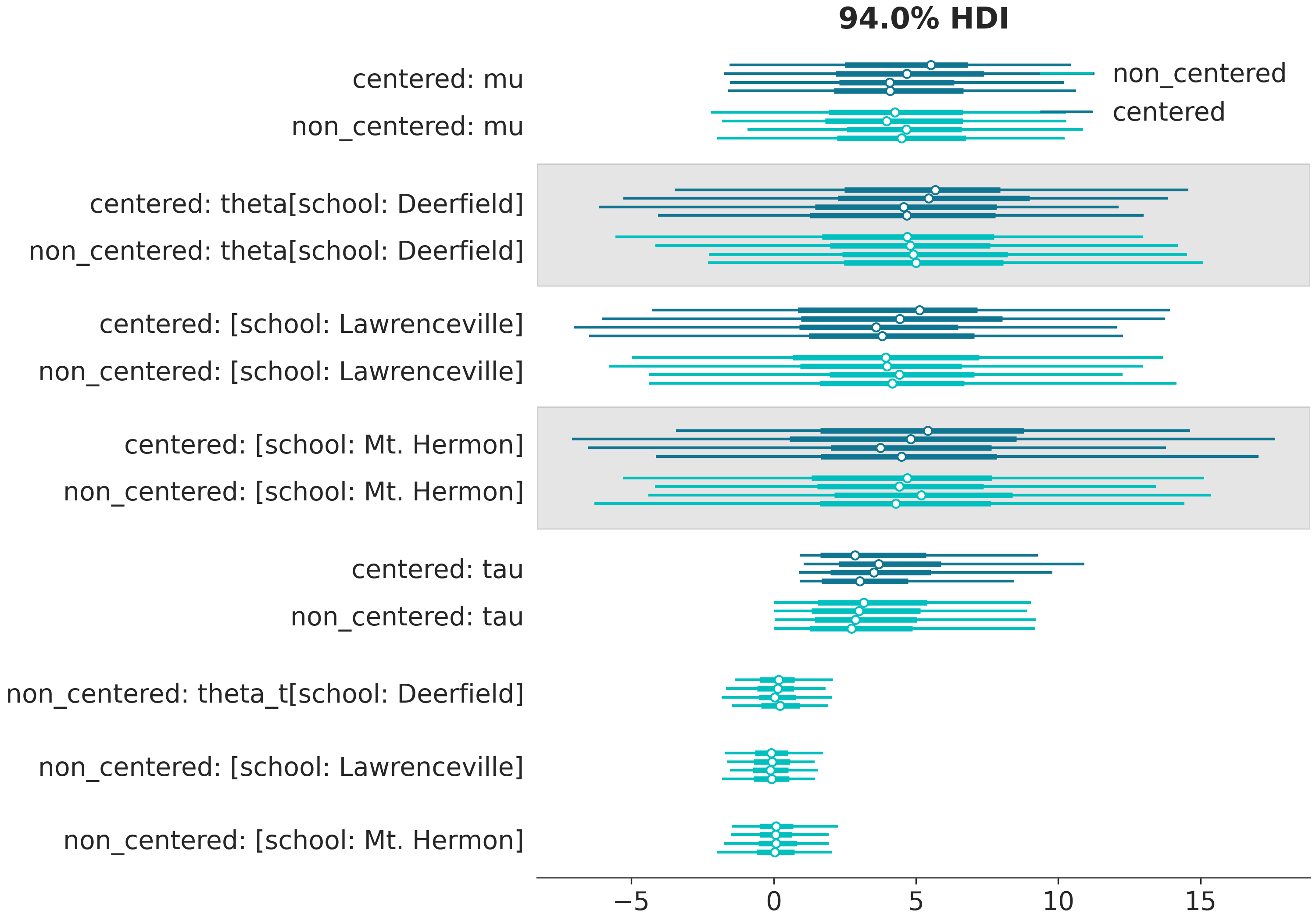
There is a lot of repeated information now.
The variable names, dims and coords are shown for both models.
Moreover, the models are labeled both in the legend and in the labels of the y axis.
For such cases, ArviZ provides a convenience function mix_labellers()
that combines labeller classes for some extra customization.
Labeller classes aim to split labeling into atomic tasks and have a method per task to maximize extensibility.
Thus, many new labellers can be created with this mixer function alone without needing to write a new class from scratch.
There are more usage examples of mix_labellers() in its docstring page, click on
it to go there.
In [20]: MixtureLabeller = azl.mix_labellers((azl.DimCoordLabeller, azl.NoModelLabeller))
In [21]: az.plot_forest(
....: (schools, schools2),
....: model_names=("centered", "non_centered"),
....: coords={"school": ["Deerfield", "Lawrenceville", "Mt. Hermon"]},
....: figsize=(10,7),
....: labeller=MixtureLabeller(),
....: legend=True
....: );
....:
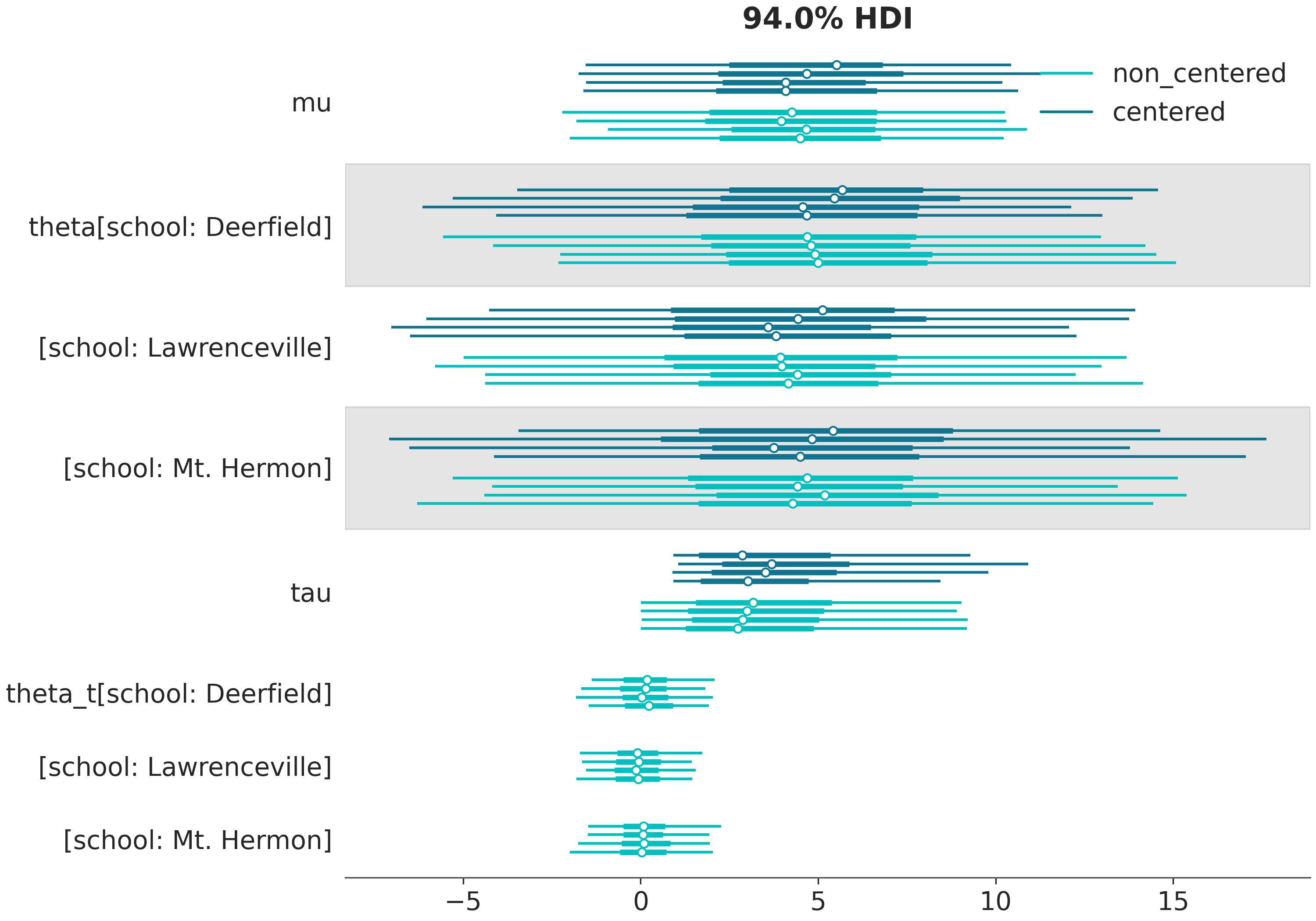
Custom labellers#
So far we have managed to customize the labels in the plots without writing a new class from scratch. However, there could be cases where we have to customize our labels further than what these sample labellers allow. In such cases, we have to subclass one of the labellers in arviz.labels and override some of its methods.
One case where we might need to do use this approach is when non indexing coordinates are present. This happens for example after doing pointwise selection on multiple dimensions, but we can also add extra dimensions to our models manually, as shown in TBD. For this example, let’s use pointwise selection. Let’s say one of the variables in the posterior represents a covariance matrix, and we want to keep it as is for other post-processing tasks instead of extracting the sub diagonal triangular matrix with no repeated info as a flattened array. Or any other pointwise selection.
Here is our data:
In [22]: from numpy.random import default_rng
In [23]: import numpy as np
In [24]: import xarray as xr
In [25]: rng = default_rng()
In [26]: cov = rng.normal(size=(4, 500, 3, 3))
In [27]: cov = np.einsum("...ij,...kj", cov, cov)
In [28]: cov[:, :, [0, 1, 2], [0, 1, 2]] = 1
In [29]: subjects = ["ecoli", "pseudomonas", "clostridium"]
In [30]: idata = az.from_dict(
....: {"cov": cov},
....: dims={"cov": ["subject", "subject bis"]},
....: coords={"subject": subjects, "subject bis": subjects}
....: )
....:
In [31]: idata.posterior
Out[31]:
<xarray.Dataset>
Dimensions: (chain: 4, draw: 500, subject: 3, subject bis: 3)
Coordinates:
* chain (chain) int64 0 1 2 3
* draw (draw) int64 0 1 2 3 4 5 6 7 ... 493 494 495 496 497 498 499
* subject (subject) <U11 'ecoli' 'pseudomonas' 'clostridium'
* subject bis (subject bis) <U11 'ecoli' 'pseudomonas' 'clostridium'
Data variables:
cov (chain, draw, subject, subject bis) float64 1.0 -1.115 ... 1.0
Attributes:
created_at: 2023-07-18T19:57:18.760542
arviz_version: 0.16.1
To select a non rectangular slice with xarray and to get the result flattened and without NaNs, we can
use DataArray s indexed with a dimension that is not present in our current dataset:
In [32]: coords = {
....: 'subject': xr.DataArray(
....: ["ecoli", "ecoli", "pseudomonas"], dims=['pointwise_sel']
....: ),
....: 'subject bis': xr.DataArray(
....: ["pseudomonas", "clostridium", "clostridium"], dims=['pointwise_sel']
....: )
....: }
....:
In [33]: idata.posterior.sel(coords)
Out[33]:
<xarray.Dataset>
Dimensions: (chain: 4, draw: 500, pointwise_sel: 3)
Coordinates:
* chain (chain) int64 0 1 2 3
* draw (draw) int64 0 1 2 3 4 5 6 7 ... 493 494 495 496 497 498 499
subject (pointwise_sel) <U11 'ecoli' 'ecoli' 'pseudomonas'
subject bis (pointwise_sel) <U11 'pseudomonas' 'clostridium' 'clostridium'
Dimensions without coordinates: pointwise_sel
Data variables:
cov (chain, draw, pointwise_sel) float64 -1.115 -0.8658 ... 1.047
Attributes:
created_at: 2023-07-18T19:57:18.760542
arviz_version: 0.16.1
We see now that subject and subject bis are no longer indexing coordinates, and
therefore won’t be available to the labeller:
In [34]: az.plot_posterior(idata, coords=coords);
To get around this limitation, we will store the coords used for pointwise selection
as a Dataset. We will pass this Dataset to the labeller so it can use the info it has available
(pointwise_sel and its position in this case) to subset this coords Dataset
and use that instead to label.
One option is to format these non-indexing coordinates as a dictionary whose
keys are dimension names and values are coordinate labels and pass that to the parent’s
sel_to_str method:
In [35]: coords_ds = xr.Dataset(coords)
In [36]: class NonIdxCoordLabeller(azl.BaseLabeller):
....: """Use non indexing coordinates as labels."""
....: def __init__(self, coords_ds):
....: self.coords_ds = coords_ds
....: def sel_to_str(self, sel, isel):
....: new_sel = {k: v.values for k, v in self.coords_ds.sel(sel).items()}
....: return super().sel_to_str(new_sel, new_sel)
....:
In [37]: labeller = NonIdxCoordLabeller(coords_ds)
In [38]: az.plot_posterior(idata, coords=coords, labeller=labeller);
This has the following advantages:
It requires very little extra code.
It allows to combine our newly created
NonIdxCoordLabellerwith other labellers as we did in the previous section.
Another option is to go for a much more customized look, and handle everything
on make_label_vert() to get labels like “Correlation between subjects x and y”.
In [39]: class NonIdxCoordLabeller(azl.BaseLabeller):
....: """Use non indexing coordinates as labels."""
....: def __init__(self, coords_ds):
....: self.coords_ds = coords_ds
....: def make_label_vert(self, var_name, sel, isel):
....: coords_ds_subset = self.coords_ds.sel(sel)
....: subj = coords_ds_subset["subject"].values
....: subj_bis = coords_ds_subset["subject bis"].values
....: return f"Correlation between subjects\n{subj} & {subj_bis}"
....:
In [40]: labeller = NonIdxCoordLabeller(coords_ds)
In [41]: az.plot_posterior(idata, coords=coords, labeller=labeller);
This won’t combine properly with other labellers, but it serves its function and
achieves complete customization of the labels, so we probably won’t want to combine
it with other labellers either. The main drawback is that we have only overridden
make_label_vert, so functions like plot_forest or summary who
use make_label_flat() will still fall back to the methods defined by BaseLabeller.