Refitting NumPyro models with ArviZ#
ArviZ is backend agnostic and therefore does not sample directly. In order to take advantage of algorithms that require refitting models several times, ArviZ uses SamplingWrapper to convert the API of the sampling backend to a common set of functions. Hence, functions like Leave Future Out Cross Validation can be used in ArviZ independently of the sampling backend used.
Below there is an example of SamplingWrapper usage for NumPyro.
import arviz as az
import numpyro
import numpyro.distributions as dist
import jax.random as random
from numpyro.infer import MCMC, NUTS
import numpy as np
import matplotlib.pyplot as plt
import scipy.stats as stats
import xarray as xr
numpyro.set_host_device_count(4)
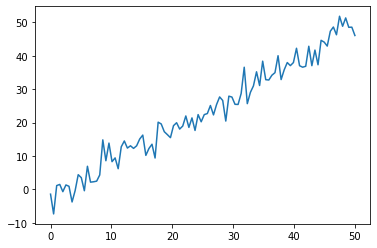
For the example, we will use a linear regression model.
np.random.seed(26)
xdata = np.linspace(0, 50, 100)
b0, b1, sigma = -2, 1, 3
ydata = np.random.normal(loc=b1 * xdata + b0, scale=sigma)
plt.plot(xdata, ydata)
[<matplotlib.lines.Line2D at 0x7f3f799141f0>]
Now we will write the NumPyro code:
def model(N, x, y=None):
b0 = numpyro.sample("b0", dist.Normal(0, 10))
b1 = numpyro.sample("b1", dist.Normal(0, 10))
sigma_e = numpyro.sample("sigma_e", dist.HalfNormal(10))
numpyro.sample("y", dist.Normal(b0 + b1 * x, sigma_e), obs=y)
We have defined a dictionary sample_kwargs that will be passed to the SamplingWrapper in order to make sure that all refits use the same sampler parameters. We follow the same pattern with az.from_numpyro.
dims = {"y": ["time"], "x": ["time"]}
idata_kwargs = {"dims": dims, "constant_data": {"x": xdata}}
idata = az.from_numpyro(mcmc, **idata_kwargs)
idata
-
- chain: 4
- draw: 1000
- chain(chain)int640 1 2 3
array([0, 1, 2, 3])
- draw(draw)int640 1 2 3 4 5 ... 995 996 997 998 999
array([ 0, 1, 2, ..., 997, 998, 999])
- b0(chain, draw)float32-3.0963688 ... -2.5883367
array([[-3.0963688, -3.1254756, -3.0458343, ..., -3.1361678, -1.0102171, -3.1635811], [-2.6088266, -2.3923745, -2.071325 , ..., -1.4179716, -2.2320666, -2.36893 ], [-2.6486611, -2.041068 , -1.2757053, ..., -1.8330991, -2.6464474, -3.0008435], [-2.2386923, -2.4664786, -2.0582101, ..., -2.6571305, -2.5223532, -2.5883367]], dtype=float32) - b1(chain, draw)float321.0462681 1.0379426 ... 1.0135907
array([[1.0462681 , 1.0379426 , 1.0442264 , ..., 1.0361298 , 0.9737489 , 1.0470366 ], [1.0280237 , 1.0181682 , 1.0067337 , ..., 0.98472387, 1.0038065 , 1.0310555 ], [1.0468849 , 0.9892221 , 0.987173 , ..., 1.0069344 , 1.028204 , 1.034664 ], [1.0255536 , 1.0160415 , 1.0144948 , ..., 1.0390292 , 1.038727 , 1.0135907 ]], dtype=float32) - sigma_e(chain, draw)float323.047911 2.6600552 ... 3.2862334
array([[3.047911 , 2.6600552, 2.6222482, ..., 3.0133255, 2.8163235, 2.7627177], [2.8674598, 2.831285 , 2.8901997, ..., 2.627824 , 3.0769517, 2.6868649], [3.2379756, 3.0725865, 2.89834 , ..., 3.2157373, 2.9057333, 2.9808404], [3.132248 , 3.134744 , 3.1434212, ..., 3.0063214, 3.0927758, 3.2862334]], dtype=float32)
- created_at :
- 2020-10-06T03:36:51.467097
- arviz_version :
- 0.10.0
- inference_library :
- numpyro
- inference_library_version :
- 0.4.0
<xarray.Dataset> Dimensions: (chain: 4, draw: 1000) Coordinates: * chain (chain) int64 0 1 2 3 * draw (draw) int64 0 1 2 3 4 5 6 7 8 ... 992 993 994 995 996 997 998 999 Data variables: b0 (chain, draw) float32 -3.0963688 -3.1254756 ... -2.5883367 b1 (chain, draw) float32 1.0462681 1.0379426 ... 1.038727 1.0135907 sigma_e (chain, draw) float32 3.047911 2.6600552 ... 3.0927758 3.2862334 Attributes: created_at: 2020-10-06T03:36:51.467097 arviz_version: 0.10.0 inference_library: numpyro inference_library_version: 0.4.0xarray.Dataset -
- chain: 4
- draw: 1000
- time: 100
- chain(chain)int640 1 2 3
array([0, 1, 2, 3])
- draw(draw)int640 1 2 3 4 5 ... 995 996 997 998 999
array([ 0, 1, 2, ..., 997, 998, 999])
- time(time)int640 1 2 3 4 5 6 ... 94 95 96 97 98 99
array([ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64, 65, 66, 67, 68, 69, 70, 71, 72, 73, 74, 75, 76, 77, 78, 79, 80, 81, 82, 83, 84, 85, 86, 87, 88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98, 99])
- y(chain, draw, time)float32-2.1860917 -3.248132 ... -2.305284
array([[[-2.1860917, -3.248132 , -2.5814402, ..., -2.0391078, -2.034887 , -2.5799031], [-2.1047454, -3.469796 , -2.6338181, ..., -1.9383975, -1.9026167, -2.4282289], [-2.0770714, -3.558466 , -2.601059 , ..., -1.8932115, -1.8839487, -2.5976093], ..., [-2.1856744, -3.241373 , -2.6004033, ..., -2.062924 , -2.02973 , -2.4057066], [-1.9645481, -4.8694654, -2.0418615, ..., -2.156882 , -2.0670033, -2.1253083], [-2.136131 , -3.3723273, -2.6302514, ..., -1.9434257, -1.9363887, -2.5883532]], [[-2.0594661, -3.6350832, -2.422883 , ..., -2.0049522, -1.9761344, -2.4362073], [-2.0196164, -3.805884 , -2.3543172, ..., -2.0218449, -1.9765555, -2.3450007], [-2.0062828, -3.9632673, -2.271522 , ..., -2.071935 , -2.0153136, -2.279218 ], ... [-2.0955684, -3.8242307, -2.274157 , ..., -2.1343343, -2.0999217, -2.385119 ], [-2.0758624, -3.5816698, -2.4365044, ..., -2.0199037, -1.9901899, -2.428019 ], [-2.1531947, -3.3295531, -2.554428 , ..., -2.0470455, -2.016633 , -2.4219239]], [[-2.0955172, -3.657714 , -2.3431501, ..., -2.0725746, -2.0606894, -2.5219502], [-2.118061 , -3.5262213, -2.403239 , ..., -2.1319387, -2.0863953, -2.3318415], [-2.0853796, -3.7505736, -2.3058176, ..., -2.1003134, -2.0711017, -2.4158561], ..., [-2.1054215, -3.50769 , -2.4407918, ..., -2.0228739, -2.0230432, -2.6089709], [-2.112451 , -3.5279531, -2.4080853, ..., -2.0487754, -2.0550582, -2.646417 ], [-2.1727455, -3.38103 , -2.4502048, ..., -2.2018573, -2.1498377, -2.305284 ]]], dtype=float32)
- created_at :
- 2020-10-06T03:36:51.544419
- arviz_version :
- 0.10.0
- inference_library :
- numpyro
- inference_library_version :
- 0.4.0
<xarray.Dataset> Dimensions: (chain: 4, draw: 1000, time: 100) Coordinates: * chain (chain) int64 0 1 2 3 * draw (draw) int64 0 1 2 3 4 5 6 7 8 ... 992 993 994 995 996 997 998 999 * time (time) int64 0 1 2 3 4 5 6 7 8 9 ... 90 91 92 93 94 95 96 97 98 99 Data variables: y (chain, draw, time) float32 -2.1860917 -3.248132 ... -2.305284 Attributes: created_at: 2020-10-06T03:36:51.544419 arviz_version: 0.10.0 inference_library: numpyro inference_library_version: 0.4.0xarray.Dataset -
- chain: 4
- draw: 1000
- chain(chain)int640 1 2 3
array([0, 1, 2, 3])
- draw(draw)int640 1 2 3 4 5 ... 995 996 997 998 999
array([ 0, 1, 2, ..., 997, 998, 999])
- diverging(chain, draw)boolFalse False False ... False False
array([[False, False, False, ..., False, False, False], [False, False, False, ..., False, False, False], [False, False, False, ..., False, False, False], [False, False, False, ..., False, False, False]])
- created_at :
- 2020-10-06T03:36:51.468495
- arviz_version :
- 0.10.0
- inference_library :
- numpyro
- inference_library_version :
- 0.4.0
<xarray.Dataset> Dimensions: (chain: 4, draw: 1000) Coordinates: * chain (chain) int64 0 1 2 3 * draw (draw) int64 0 1 2 3 4 5 6 7 ... 992 993 994 995 996 997 998 999 Data variables: diverging (chain, draw) bool False False False False ... False False False Attributes: created_at: 2020-10-06T03:36:51.468495 arviz_version: 0.10.0 inference_library: numpyro inference_library_version: 0.4.0xarray.Dataset -
- time: 100
- time(time)int640 1 2 3 4 5 6 ... 94 95 96 97 98 99
array([ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64, 65, 66, 67, 68, 69, 70, 71, 72, 73, 74, 75, 76, 77, 78, 79, 80, 81, 82, 83, 84, 85, 86, 87, 88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98, 99])
- y(time)float64-1.412 -7.319 1.151 ... 48.52 46.03
array([-1.41202037, -7.3186587 , 1.15145745, 1.50159596, -0.66638434, 1.340505 , 0.94309618, -3.74339279, -0.34243761, 4.41332204, 3.52852595, -0.38735502, 6.92937569, 2.17738437, 2.29506712, 2.479826 , 4.32780469, 14.8236344 , 8.58376674, 13.86029246, 8.30748541, 9.42697384, 6.20130931, 12.74674786, 14.49628457, 12.37415809, 13.04994867, 12.27711609, 13.04606435, 15.07724923, 16.25148031, 10.18710661, 12.24013837, 13.51964002, 9.40025182, 20.11401051, 19.57963549, 17.26609676, 16.39293544, 15.4848222 , 19.07510716, 19.94747454, 18.05554676, 18.95703705, 21.97194249, 18.55533794, 21.38972486, 17.64270549, 22.38207915, 20.23227438, 22.3752402 , 22.69176278, 25.10069955, 22.29368553, 25.38288326, 27.6663142 , 26.60546597, 20.45069871, 27.89511126, 27.62673933, 25.45690863, 25.41379887, 28.68450485, 36.54353412, 25.65553597, 29.01507728, 30.97776362, 35.17952383, 31.07761309, 38.35764652, 32.82119153, 32.72583667, 34.15217468, 34.91746821, 39.98665155, 32.85510289, 35.76383771, 37.94409775, 37.02228539, 37.94068802, 42.21713708, 36.9942534 , 36.55582315, 36.82877733, 42.81862081, 37.00939662, 41.67250008, 37.28144053, 44.59191824, 44.05883374, 42.87139157, 47.30850894, 48.57268519, 46.25413295, 51.7918344 , 48.79686829, 51.28945751, 48.48599342, 48.52212075, 46.03052542])
- created_at :
- 2020-10-06T03:36:51.545286
- arviz_version :
- 0.10.0
- inference_library :
- numpyro
- inference_library_version :
- 0.4.0
<xarray.Dataset> Dimensions: (time: 100) Coordinates: * time (time) int64 0 1 2 3 4 5 6 7 8 9 ... 90 91 92 93 94 95 96 97 98 99 Data variables: y (time) float64 -1.412 -7.319 1.151 1.502 ... 48.49 48.52 46.03 Attributes: created_at: 2020-10-06T03:36:51.545286 arviz_version: 0.10.0 inference_library: numpyro inference_library_version: 0.4.0xarray.Dataset -
- time: 100
- time(time)int640 1 2 3 4 5 6 ... 94 95 96 97 98 99
array([ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64, 65, 66, 67, 68, 69, 70, 71, 72, 73, 74, 75, 76, 77, 78, 79, 80, 81, 82, 83, 84, 85, 86, 87, 88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98, 99])
- x(time)float640.0 0.5051 1.01 ... 49.49 50.0
array([ 0. , 0.50505051, 1.01010101, 1.51515152, 2.02020202, 2.52525253, 3.03030303, 3.53535354, 4.04040404, 4.54545455, 5.05050505, 5.55555556, 6.06060606, 6.56565657, 7.07070707, 7.57575758, 8.08080808, 8.58585859, 9.09090909, 9.5959596 , 10.1010101 , 10.60606061, 11.11111111, 11.61616162, 12.12121212, 12.62626263, 13.13131313, 13.63636364, 14.14141414, 14.64646465, 15.15151515, 15.65656566, 16.16161616, 16.66666667, 17.17171717, 17.67676768, 18.18181818, 18.68686869, 19.19191919, 19.6969697 , 20.2020202 , 20.70707071, 21.21212121, 21.71717172, 22.22222222, 22.72727273, 23.23232323, 23.73737374, 24.24242424, 24.74747475, 25.25252525, 25.75757576, 26.26262626, 26.76767677, 27.27272727, 27.77777778, 28.28282828, 28.78787879, 29.29292929, 29.7979798 , 30.3030303 , 30.80808081, 31.31313131, 31.81818182, 32.32323232, 32.82828283, 33.33333333, 33.83838384, 34.34343434, 34.84848485, 35.35353535, 35.85858586, 36.36363636, 36.86868687, 37.37373737, 37.87878788, 38.38383838, 38.88888889, 39.39393939, 39.8989899 , 40.4040404 , 40.90909091, 41.41414141, 41.91919192, 42.42424242, 42.92929293, 43.43434343, 43.93939394, 44.44444444, 44.94949495, 45.45454545, 45.95959596, 46.46464646, 46.96969697, 47.47474747, 47.97979798, 48.48484848, 48.98989899, 49.49494949, 50. ])
- created_at :
- 2020-10-06T03:36:51.545865
- arviz_version :
- 0.10.0
- inference_library :
- numpyro
- inference_library_version :
- 0.4.0
<xarray.Dataset> Dimensions: (time: 100) Coordinates: * time (time) int64 0 1 2 3 4 5 6 7 8 9 ... 90 91 92 93 94 95 96 97 98 99 Data variables: x (time) float64 0.0 0.5051 1.01 1.515 ... 48.48 48.99 49.49 50.0 Attributes: created_at: 2020-10-06T03:36:51.545865 arviz_version: 0.10.0 inference_library: numpyro inference_library_version: 0.4.0xarray.Dataset
We will create a subclass of az.SamplingWrapper. Therefore, instead of having to implement all functions required by reloo() we only have to implement sel_observations() (we are cloning sample() and get_inference_data() from the PyStanSamplingWrapper in order to use apply_ufunc() instead of assuming the log likelihood is calculated within Stan).
Let’s check the 2 outputs of sel_observations.
data__iis a dictionary because it is an argument ofsamplewhich will pass it as is tomodel.sampling.data_exis a list because it is an argument tolog_likelihood__iwhich will pass it as*data_extoapply_ufunc.
More on data_ex and apply_ufunc integration is given below.
class NumPyroSamplingWrapper(az.SamplingWrapper):
def __init__(self, model, **kwargs):
self.model_fun = model.sampler.model
self.rng_key = kwargs.pop("rng_key", random.PRNGKey(0))
super(NumPyroSamplingWrapper, self).__init__(model, **kwargs)
def log_likelihood__i(self, excluded_obs, idata__i):
samples = {
key: values.values.reshape((-1, *values.values.shape[2:]))
for key, values in idata__i.posterior.items()
}
log_likelihood_dict = numpyro.infer.log_likelihood(self.model_fun, samples, **excluded_obs)
if len(log_likelihood_dict) > 1:
raise ValueError("multiple likelihoods found")
data = {}
nchains = idata__i.posterior.dims["chain"]
ndraws = idata__i.posterior.dims["draw"]
for obs_name, log_like in log_likelihood_dict.items():
shape = (nchains, ndraws) + log_like.shape[1:]
data[obs_name] = np.reshape(log_like.copy(), shape)
return az.dict_to_dataset(data)[obs_name]
def sample(self, modified_observed_data):
self.rng_key, subkey = random.split(self.rng_key)
mcmc = MCMC(**self.sample_kwargs)
mcmc.run(subkey, **modified_observed_data)
return mcmc
def get_inference_data(self, fit):
# Cloned from PyStanSamplingWrapper.
idata = az.from_numpyro(mcmc, **self.idata_kwargs)
return idata
class LinRegWrapper(NumPyroSamplingWrapper):
def sel_observations(self, idx):
xdata = self.idata_orig.constant_data["x"].values
ydata = self.idata_orig.observed_data["y"].values
mask = np.isin(np.arange(len(xdata)), idx)
data__i = {"x": xdata[~mask], "y": ydata[~mask], "N": len(ydata[~mask])}
data_ex = {"x": xdata[mask], "y": ydata[mask], "N": len(ydata[mask])}
return data__i, data_ex
loo_orig = az.loo(idata, pointwise=True)
loo_orig
Computed from 4000 by 100 log-likelihood matrix
Estimate SE
elpd_loo -250.92 7.20
p_loo 3.11 -
------
Pareto k diagnostic values:
Count Pct.
(-Inf, 0.5] (good) 100 100.0%
(0.5, 0.7] (ok) 0 0.0%
(0.7, 1] (bad) 0 0.0%
(1, Inf) (very bad) 0 0.0%
In this case, the Leave-One-Out Cross Validation (LOO-CV) approximation using Pareto Smoothed Importance Sampling (PSIS) works for all observations, so we will use modify loo_orig in order to make az.reloo believe that PSIS failed for some observations. This will also serve as a validation of our wrapper, as the PSIS LOO-CV already returned the correct value.
loo_orig.pareto_k[[13, 42, 56, 73]] = np.array([0.8, 1.2, 2.6, 0.9])
We initialize our sampling wrapper. Let’s stop and analyze each of the arguments.
We use
idata_origas a starting point, and mostly as a source of observed and constant data which is then subsetted insel_observations.We also use
modelto get automatic log likelihood computation and we have the option to set therng_key. Even if the data for each fit is different therng_keyis split with every fit.Finally,
sample_kwargsandidata_kwargsare used to make sure all refits and correspondingInferenceDataare generated with the same properties.
numpyro_wrapper = LinRegWrapper(
mcmc,
rng_key=random.PRNGKey(5),
idata_orig=idata,
sample_kwargs=sample_kwargs,
idata_kwargs=idata_kwargs,
)
And eventually, we can use this wrapper to call az.reloo, and compare the results with the PSIS LOO-CV results.
loo_relooed = az.reloo(numpyro_wrapper, loo_orig=loo_orig)
/home/oriol/miniconda3/envs/arviz/lib/python3.8/site-packages/arviz/stats/stats_refitting.py:99: UserWarning: reloo is an experimental and untested feature
warnings.warn("reloo is an experimental and untested feature", UserWarning)
arviz.stats.stats_refitting - INFO - Refitting model excluding observation 13
INFO:arviz.stats.stats_refitting:Refitting model excluding observation 13
arviz.stats.stats_refitting - INFO - Refitting model excluding observation 42
INFO:arviz.stats.stats_refitting:Refitting model excluding observation 42
arviz.stats.stats_refitting - INFO - Refitting model excluding observation 56
INFO:arviz.stats.stats_refitting:Refitting model excluding observation 56
arviz.stats.stats_refitting - INFO - Refitting model excluding observation 73
INFO:arviz.stats.stats_refitting:Refitting model excluding observation 73
loo_relooed
Computed from 4000 by 100 log-likelihood matrix
Estimate SE
elpd_loo -250.89 7.20
p_loo 3.08 -
------
Pareto k diagnostic values:
Count Pct.
(-Inf, 0.5] (good) 100 100.0%
(0.5, 0.7] (ok) 0 0.0%
(0.7, 1] (bad) 0 0.0%
(1, Inf) (very bad) 0 0.0%
loo_orig
Computed from 4000 by 100 log-likelihood matrix
Estimate SE
elpd_loo -250.92 7.20
p_loo 3.11 -
------
Pareto k diagnostic values:
Count Pct.
(-Inf, 0.5] (good) 96 96.0%
(0.5, 0.7] (ok) 0 0.0%
(0.7, 1] (bad) 2 2.0%
(1, Inf) (very bad) 2 2.0%
